Which form is the universe?

When you look at your surrounding environment, it might look like living in a flat plane. After all, that’s why you can navigate a new city that uses a map: a piece of flat paper that represents all of the places around you. This is probably because some people in the past believed that the land is flat. But most people know it’s far from the truth.

You live on the surface of a giant sphere, like a shore ball the dirt size with few bumps added. The surface of the sphere and plane are two possible 2D spaces, which means you can walk in two directions: the north and south or east.

What other possible spaces could you be alive? Is that other spaces around you are 2d? For example, the surface of a giant donut is another space 2D.

Through a field called geometric topology, mathematics i like You study all possible spaces in all sizes. Either tried to designate sensor safe network, My data or use Origas to deplicate satellitesThe underlying language and ideas are likely to be the one of the topology.

The form of the universe

When you get around the universe living, it looks like a 3D space, as the land surface makes a 2D area. However, as well as the Earth, if you had to look at the universe, it could be a more complicated area, as a 2D’s fair’s fair-saddle version

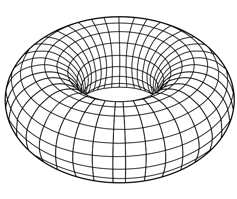
While you don’t need to topology to determine that you live on something like a giant beach ball, knowing all possible 2d spaces can be useful. Over a century ago, math have thought all possible spaces 2d and a lot of their properties.

In the past several decades, mathematicians learned a lot of all possible 3D spaces. While we don’t have a complete understanding as us for us for 2D spaces, we do to know a lot. I am With this knowledge, physical and the astronomers can try to determine what The people of the 3D space really live. I am

While the answer is not known, there are many intrigating and surprising possessions. I am The options just become more complicated if you consider the time as a size.

To see how this may work, notice that to describe the place of something in the space – you need four numbers: three to describe their position and one to describe the time. These four numbers are what makes up a 4D space.

Now, you can consider what 4D spaces are possible and in which of those are living.

Topology in higher sizes

In this point, can seem that there is no reason to consider the spaces that have sizes greater than four, from that is the least imaginable you could describe our university. But a branch of physical called String’s theory suggest that the universe has many more dimensions from four.

There are also practical applications of thinking higher-sized areas, as The schedule of robot movement. I am Suppose you are trying to understand three robots movement that move around a factory plan in a warehouse. You can put a grid on the floor and describe each of the robot’s position by its and y and y and y-coordinates, you need six numbers to describe all the possible robots. You can interpret the possible positions of robots as a 6d space.

Since robot number increases, the size of space increases. Fact in other information useful, as the obstacle locations, makes the most complicated space. To study this problem, you need to study high-dimensional spaces.

Are not innumered other scientific problems where they appear lifting spaces, from modeling moving to planets and the spacecraft to try to understand the “Form” of great Datasets. I am

Attached in nodes

Another type of trouble problem problems is as you can stay in another.

For example, if you have a rope cycle, then we have a 1D area (the rope loop) within a 3D space (your room). Such laws are called math nodes.

The one’s I study nodes The first grown by physics but became a central area of ​​the topology. Are indispensable to how the scientists understand 3d spaces and 4d and have a delicious and suck structure that researchers are always trying to understand. I am

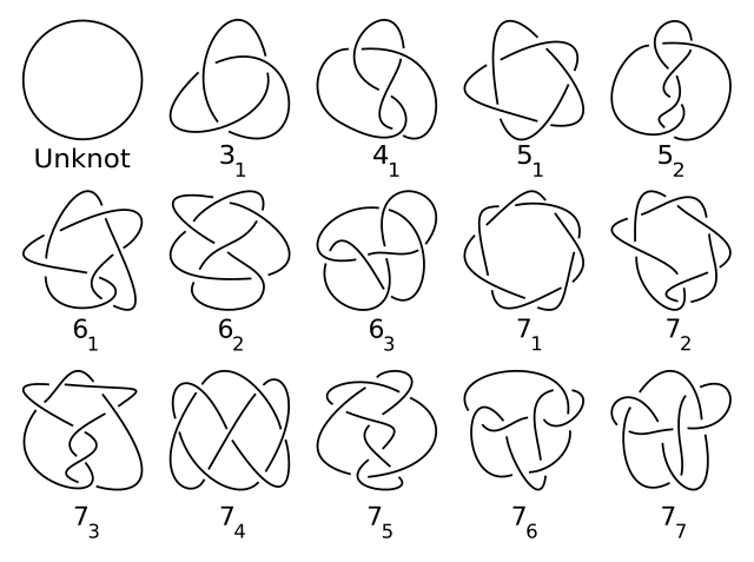
Also, knots have many applications, which ranges from String’s theory In physics to AMna Recommend in biology to Chatraction in chemistry.

What form do you live in?

The geometric toop is a beautiful and complex subject, and there are always without confining exciting questions to answer the spaces.

For example, the Pointaré conjecture smooth Asks what “simplest” closed “space is, and the conjecture of the slice Aim to understand how nodes in 3D spaces relating to the surface in 4D spaces.

Topology is currently useful in science and engineering. Unraveling more mysteries in all sizes will be inestable to understand the world in which we live and solve the problems of real world.

John HynyMath teacher, Georgia’s Technology Institute

This item is republished by The conversation under a creative common license. Read the Original article. I am